Merge Sort algorithm

Merge Sort is a kind of Divide and Conquer algorithm in computer programrming. It is one of the most popular sorting algorithms and a great way to develop confidence in building recursive algorithms.

Divide and Conquer Strategy

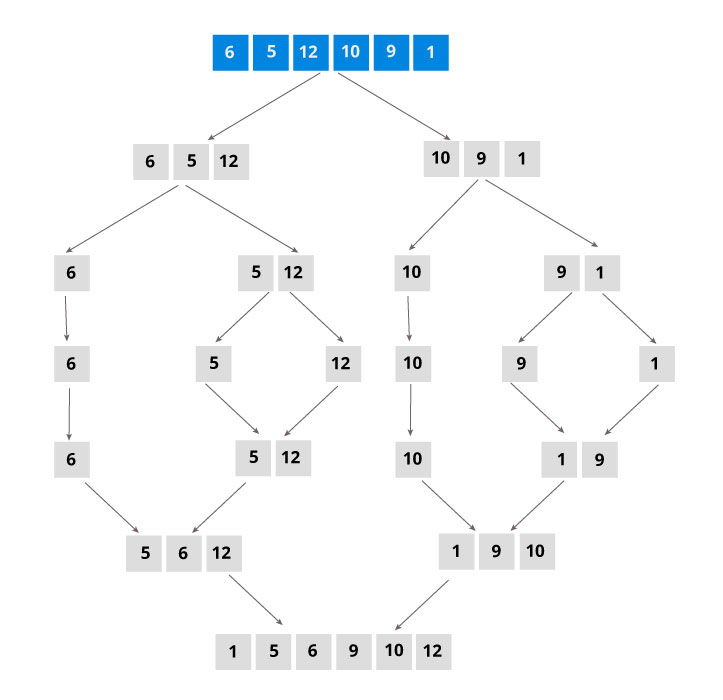
Using the Divide and Conquer technique, we divide a problem into subproblems. When the solution to each subproblem is ready, we 'combine' the results from the subproblems to solve the main problem.

Suppose we had to sort an array A. A subproblem would be to sort a sub-section of this array starting at index p and ending at index r, denoted as A[p..r].

Divide

 

If q is the half-way point between p and r, then we can split the subarray A[p..r] into two arrays A[p..q] and A[q+1, r].

 

Conquer

 

In the conquer step, we try to sort both the subarrays A[p..q] and A[q+1, r]. If we haven't yet reached the base case, we again divide both these subarrays and try to sort them.

 

Combine

 

When the conquer step reaches the base step and we get two sorted subarrays A[p..q] and A[q+1, r] for array A[p..r], we combine the results by creating a sorted array A[p..r] from two sorted subarrays A[p..q] and A[q+1, r]

Merge function explained step-by-step

There is a lot happening in this function, so let's take an example to see how this would work.

As usual, a picture speaks a thousand words.

The array A[0..8] contains two sorted subarrays A[1..5] and A[6..7]. Let us see how merge function will merge the two arrays.

void merge(int A[], int p = 1, int q = 4, int 6)
{

Step 1: Create duplicate copies of sub-arrays to be sorted

    /* Create L ← A[p..q] and M ← A[q+1..r] */
    n1 = 4 - 1 + 1 = 4;
    n2 =  6 - 4 = 2;
 
    int L[4], M[2];

    for (i = 0; i < 4; i++)
        L[i] = A[p + i];
    /* L[0,1,2,3] = A[1,2,3,4] = [1,5,10,12] */

    for (j = 0; j < 2; j++)
        M[j] = A[q + 1 + j];
    /* M[0,1,2,3] = A[5,6] = [6,9]

Step 2: Maintain current index of sub-arrays and main array

    
    int i, j, k;
    i = 0; 
    j = 0; 
    k = p; 

Step 3: Until we reach end of either L or M, pick larger among elements L and M and place them in the correct position at A[p..r]

    while (i < n1 && j < n2) { 
        if (L[i] <= M[j]) { 
            A[k] = L[i]; i++; 
        } 
        else { 
            A[k] = M[j]; 
            j++; 
        } 
        k++; 
    }

Step 4: When we run out of elements in either L or M, pick up the remaining elements and put in A[p..r]

/* We exited the earlier loop because j < n2 doesn't hold */  
    while (i < n1)
    {
        A[k] = L[i];
        i++;
        k++;
    }

/* We exited the earlier loop because i < n1 doesn't hold */  
 
    while (j < n2)
    {
        A[k] = M[j];
        j++;
        k++;
    }
}

This step would have been needed if size of M was greater than L.

At the end of the merge function, the subarray A[p..r] is sorted.